Quantum networks form the key component of both distributed quantum computing and quantum communication as it helps us to transfer quantum as well as classical information. Last couple of years we have seen significant advancement of quantum technology. We are able to establish different quantum networks either by free-space satellite based technologies or by repeater based technology in ground to ground stations based scenarios. These all will lead us to the establishment of the quantum internet which is the ultimate goal.

Our Contributions

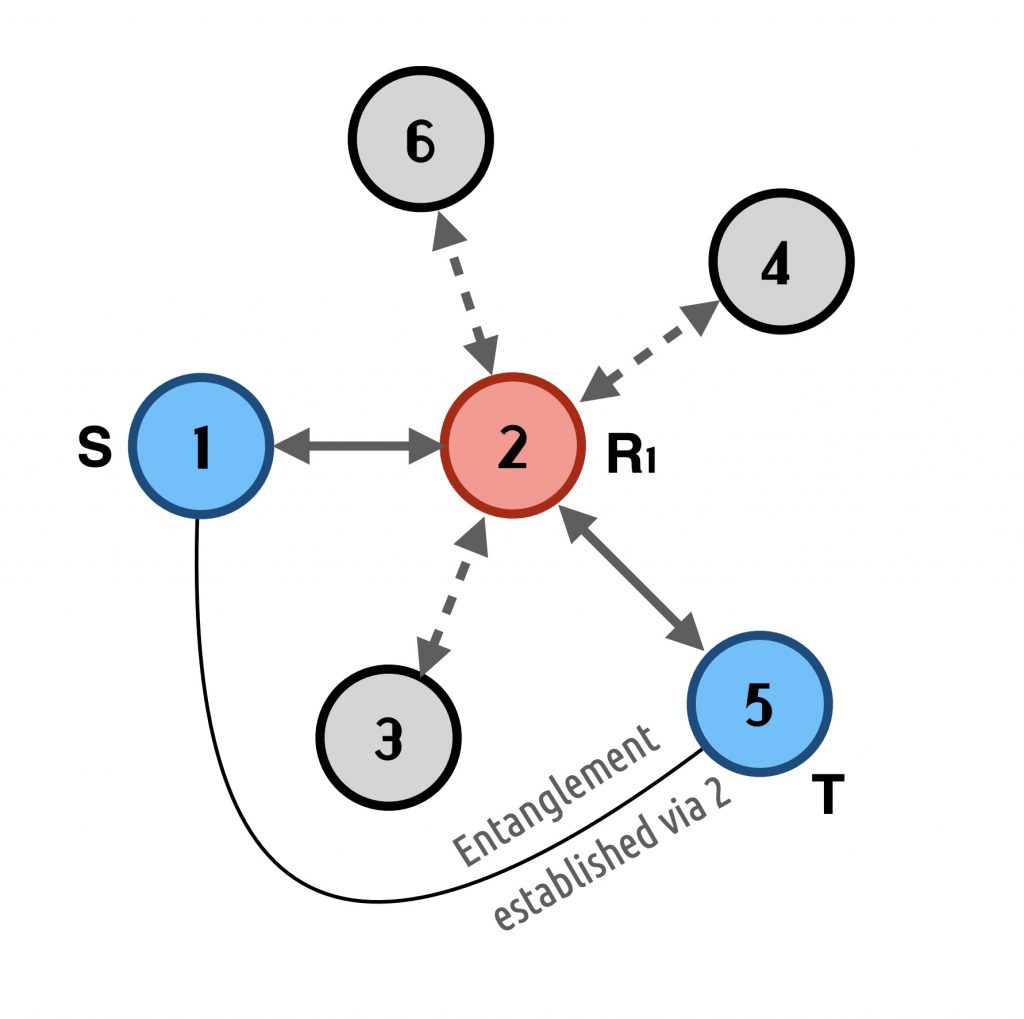
Topology of Quantum Networks

Quantum technologies enable us to establish quantum networks which will finally pave the way towards full stack quantum internet. This can either be established by free-space satellite based technologies or by repeater based technology in a ground to ground stations based scenario. It is interesting to see whether network topology will play a significant role in the efficacy of quantum networks, when we move from simple scenarios to more complicated scenarios. One of the researches carried out is to see whether network topology will play a significant role in the efficacy of quantum networks, when we move from simple networks to more complex networks.

In a repeater based quantum network scenario we are able to create a global metric to quantify the network’s ability to do distributed teleportation. These are done with different network topologies starting from loopless trees to network with loops. We also investigate non classicality of quantum network correlations (repeater based) in presence of different types of noise. [1,2]

Characterisation of
Resources for Quantum Communication

One of the most important aspects of quantum communication is the resource characterisation. As an example we can think about quantum entanglement as a resource for quantum communication. However the resource may not be limited to entanglement. Resources can also be those states which are explicitly useful for certain tasks like teleportation and super dense coding. It is also important to find out states that are not yet useful but can be made useful after application of quantum operations. In that context building up a resource theory for these resources becomes important with the classification of free operations and free state.

We are able to construct the witness operators to detect the states with negative conditional entropy. This was done after we have proved the existence of the witness. This helps us to detect the states with negative conditional entropy states. We are also able to detect the states that are not useful but can be made useful after the application of a global unitary operator. In that process we have identified the states that are resilient to the action of global unitary operators. [3,4]

Broadcasting of correlations
in a Quantum World

Entanglement and other measures of correlation play a significant role in accessing the state’s ability in quantum communication. In a sense, purer the entanglement more valuable it is. As a consequence of which distillation of pure quantum entanglement from partially entangled states is considered to be an important task. However when we require more number of entangled states between two parties we simply ask the question : If decompression of quantum correlation is possible or not. This process of decompression of quantum correlations is known as “Broadcasting of Quantum Correlations”. The process helps us to create more entangled states with lesser entanglement between two quantum processors It is interesting to see to what extent we are able to broadcast correlations starting with different quantum states to start with.

We are able to implement the broadcasting of entanglement present in a general two qubit state. This is done with the help of both local and nonlocal symmetric and asymmetric cloner . Our results also extend beyond qubit systems to 2 x d systems and for NPT entangled states in 3×3 systems. We have also worked with broadcasting of quantum coherence and quantum correlation beyond the notion of entanglement [5–10]

Quantum Secret Sharing

The idea of secret sharing is nothing but to share a secret between people who can not reveal the secret unless all the parties collaborate. In a simple three party scenario, the dealer shares secrets with two parties in such a way that nobody will be able to reveal the secret without invoking the other parties. This is a very useful technique if one of the parties is dishonest. Quantum secret sharing generally deals with the problem of sharing both classical as well as quantum secrets.

We are able to differentiate between quantum secret sharing (QSS) and the general controlled state reconstruction (CSR) by providing tighter conditions for secret sharing. This is added up with a closed expression formula for the quantum state reconstruction which eventually he;p us to characterise the states that can act as a resource both for CSR and QSS. We are able to identify the best candidate among the secret sharing resource states in achieving the maximum reconstruction fidelity thus by setting the practical information transfer limit. [11,12]

References

[1] Teleportation fidelity of quantum repeater networks, Ganesh Mylavarapu, Subrata Ghosh, Chittaranjan Hens, Indranil Chakrabarty, Subhadip Mitra, Phys. Rev. A 112, 032618 (2025).

[2] Persistency Of Non n-Local Correlations In Noisy Linear Networks, Kaushiki Mukherjee, Indranil Chakrabarty, Ganesh Mylavarappu, Phys. Rev. A 107, 032404 (2023).

[3] Witnessing Negative Conditional Entropy, Mahati Vempati, Nirman Ganguly, Indranil Chakrabarty, Arun K Pati, Phys. Rev. A 104, 012417 (2021).

[4] Non-negativity of conditional von Neumann entropy and global unitary operations, Subhasree Patro, Indranil Chakrabarty, Nirman Ganguly, Phys. Rev. A 96, 062102 (2017).

[5] Broadcasting of Quantum Correlations: Possibilities and Impossibilities, S. Chatterjee, S. Sazim, I. Chakrabarty, Phys. Rev. A 93, 042309 (2016).

[6] Broadcasting Quantum Coherence via Cloning, Indranil Chakrabarty, Udit Kamal Sharma, Manish Kumar Shukla, Phys. Rev. A 96, 052319 (2017).

[7] Asymmetric broadcasting of quantum correlations, Aditya Jain, Indranil Chakrabarty, and Sourav Chatterjee, Phys. Rev. A 99, 022315 (2019).

[8] Broadcasting of quantum correlations in qubit-qudit systems, Rounak Mundra, Dhrumil Patel, Indranil Chakrabarty, Nirman Ganguly, Sourav Chatterjee, Phys. Rev. A 100, 042319 (2019) .

[9] Broadcasting of NPT Entanglement in Two Qutrit Systems, Rounak Mundra, Sabuj Chattopadhyay, Indranil Chakrabarty, Nirman Ganguly, Pramana – J Phys 95, 60 (2021).

[10] Broadcasting of entanglement via orthogonal & non-orthogonal state dependent cloners, Manish Kumar Shukla, Indranil Chakrabarty, Sourav Chatterjee, Quantum Inf Process, 19, 15 (2020) .

[11] Controlled state reconstruction and quantum secret sharing, Pahulpreet Singh and Indranil Chakrabarty, Phys. Rev. A 109, 032406 (2024).

[12] Maximal Secret Reconstruction, Teleportation and Bell’s Inequality, Pratishtha Abrol, Pahulpreet Singh, Indranil Chakrabarty, Eur. Phys. J. D, 79, 11 (2025).

Last edited: Sep 30, 2025
Contributor(s): Indranil Chakrabarty